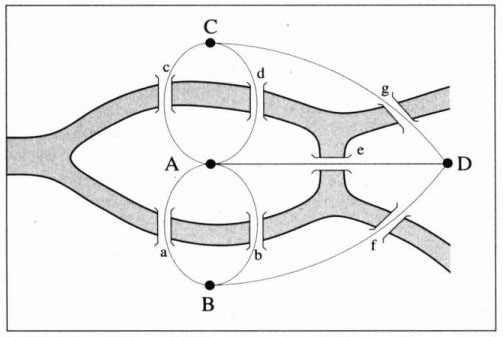
Strange as it may sound, the study of networks began for me in 7th grade with geometry and algebra. Little did I know the Konigsberg Bridge problem would reappear in my life in a more meaningful way 15 years later. It is interesting to think of this problem as being fundamental in the way we now graph network typologies: nodes and edges. But beyond pure representational techniques, this problem represents an early venture into abstraction. To reduce places and routes – physical things – down to mere points and lines is fundamental in understanding other abstract concepts like: efficiency, connectivity, the small-world effect, etc. Philip Ball expands on this in Web Worlds , that this system of representation can be extended to diagramming natural phenomena (fluvial) as well as the man-made (telephony, electrical grids). Surely, graph theory is one of the first layers of the anthropocene – an indelible mark left on the earth, by us. Thanks to Leonhard Euler, the author of the Konigsberg Bridge problem, biological and synthetic can be understood in the same visual language.